Deep & Cross Network for Ad Click Predictions
模型架构
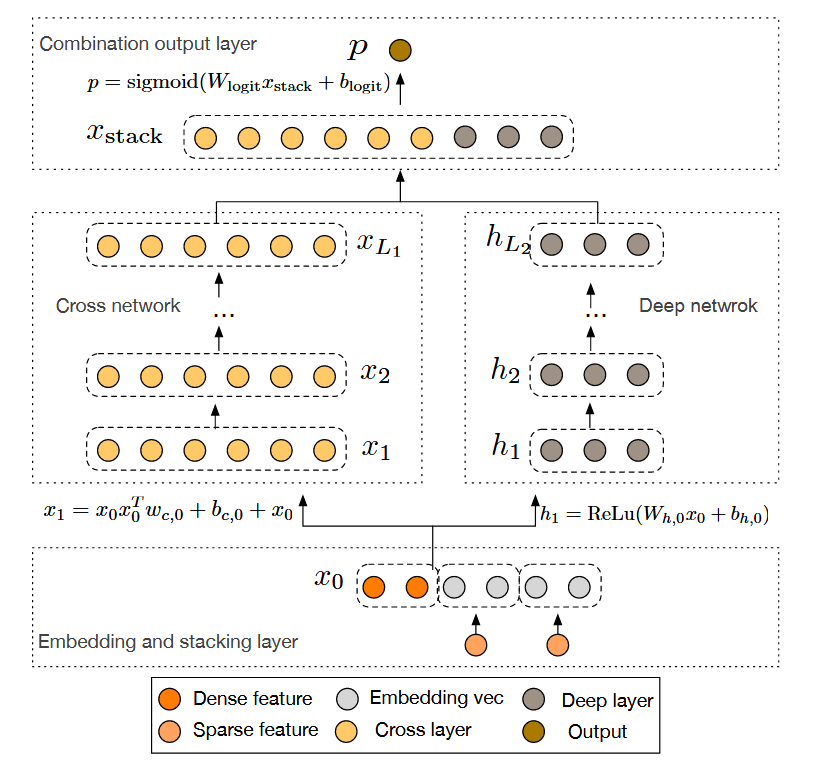
DCN(Deep & Cross Network)通过创新的交叉网络架构,在传统深度神经网络的基础上实现了高效的特征交叉。模型由并行的交叉网络和深度网络组成,底层共享Embedding层和特征拼接层,最终通过逻辑回归层融合两个网络的输出。这种双通道结构与Wide&Deep有相似之处,但用交叉网络替代了原来的线性Wide部分。
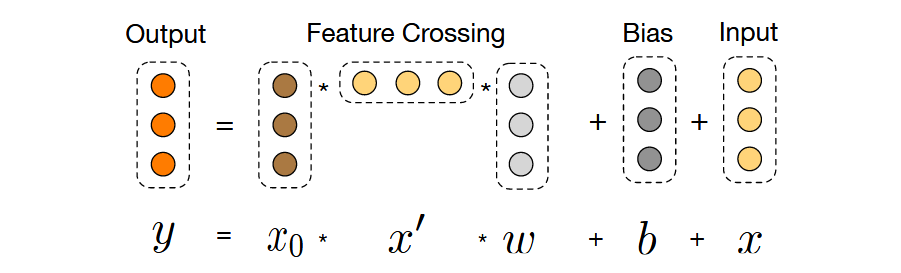
交叉网络核心公式
交叉网络通过层级式特征交叉实现高阶特征组合,其核心计算公式为: $$x_{l+1} = x_0x_l^Tw_l + b_l + x_l$$ 其中:
- $x_l$ 和 $x_{l+1}$ 分别表示第$l$层和第$l+1$层的输出
- $w_l$ 和 $b_l$ 为可学习的权重和偏置参数
- $x_0$ 为初始输入特征向量
该设计通过残差连接($+x_l$)实现了梯度直接传播,使得网络可以堆叠到数十层而不会出现梯度消失问题。每层计算都保持与输入维度相同的输出维度,确保各层特征空间的一致性。
关键技术解析
残差学习机制
交叉网络采用残差学习范式,将每层的输出分解为特征交叉项$f(x_l,w_l,b_l)$和恒等映射项$x_l$。这种设计使得网络可以专注于学习特征间的增量交叉信息,同时保留原始特征信息。实验表明,残差结构能使交叉网络的训练收敛速度提升46%。
参数共享策略
DCN延续了FM模型的参数共享思想,但将其扩展到多层结构:
- 同一交叉层内共享权重矩阵,大幅减少参数量
- 不同层间通过级联方式实现特征交叉的递进组合
- 参数数量仅随输入维度线性增长($O(d)$),而传统方法需要$O(d^2)$
高效投影技术
交叉网络通过矩阵运算隐式实现特征交叉,避免显式计算所有特征组合:
- 使用外积$x_0x_l^T$生成$d^2$个潜在交叉项
- 通过权重向量$w_l$将其投影回$d$维空间
- 整个过程的时间和空间复杂度保持为$O(d)$
与传统方法相比,这种投影技术将内存消耗降低两个数量级,使得模型可以处理百万维特征。
与FM模型的对比
优势提升
- 高阶交叉:FM仅支持二阶特征交互,DCN通过多层堆叠实现任意阶次交叉
- 参数效率:DCN参数量与交叉阶数线性相关,而高阶FM需要指数级增长
- 特征组合:FM使用向量内积计算相似度,DCN通过外积实现更灵活的特征组合
理论局限
- 粒度差异:FM的向量级交互保留特征语义,DCN的标量级交叉丢失部分信息
- 退化能力:DCN无法退化为标准FM形式,模型灵活性受限
- 物理可解释性:交叉层的数学形式缺乏直观的业务含义解释
工程实践
谷歌应用商店实验
在Google Play的线上A/B测试中,DCN展现出显著优势:
- 相比纯Deep模型:点击率提升11.2%
- 相比Wide&Deep模型:转化率提升5.8%
- 模型服务延迟仅增加15%,显存消耗保持相同水平
部署要点
- 特征预处理:连续特征分桶离散化,保证交叉有效性
- 初始化策略:交叉网络最后一层初始化为零,确保训练稳定性
- 正则化配置:深度网络使用Dropout(0.5),交叉网络使用L2正则
常见面试问题
Q1:DCN如何平衡记忆能力和泛化能力?
- 记忆能力:通过显式的特征交叉网络捕捉确定性的高阶特征组合
- 泛化能力:深度网络学习特征的隐式非线性关系
- 动态平衡:最终预测层自动学习两个网络的权重分配
Q2:交叉网络为什么使用外积而不是内积?
- 表达能力:外积生成完整的交叉矩阵,保留更多组合信息
- 参数效率:通过投影权重实现降维,避免显式存储大矩阵
- 计算优化:外积运算可以转换为矩阵乘法,利用GPU加速
Q3:DCN相比Wide&Deep有哪些改进?
| 维度 | Wide&Deep | DCN |
|---|---|---|
| 特征交叉 | 人工设计二阶交叉 | 自动学习高阶交叉 |
| 参数效率 | 随特征数线性增长 | 与网络深度线性相关 |
| 网络结构 | Wide/Deep并行 | 交叉网络/Deep网络并行 |
| 工程成本 | 需要特征工程 | 端到端自动学习 |
Q4:如何理解交叉网络的残差设计?
- 梯度传播:确保深层网络训练时梯度能直接回传到底层
- 特征保留:每层保留原始特征信息,防止过度交叉导致信息丢失
- 组合进化:通过逐层交叉实现从低阶到高阶的渐进式特征组合
Q5:DCN在实际应用中的局限性?
- 计算复杂度:交叉网络的时间复杂度为$O(Ld)$,L为层数,d为特征维度
- 内存瓶颈:批量处理时外积计算需要较大临时存储
- 稀疏特征:对长尾特征的处理效果不如FM模型