ReLU (Rectified Linear Unit)

简单的门限函数，负值置零 $$\text{ReLU}(x) = \max(0, x) = \begin{cases} x & \text{if } x > 0 \ 0 & \text{if } x \leq 0 \end{cases}$$

起源：2010年由Nair和Hinton在论文"Rectified Linear Units Improve Restricted Boltzmann Machines"中提出

优点：

• 计算简单，训练快速（只需判断是否大于0）
• 有效缓解梯度消失问题（正值区域梯度恒为1）
• 产生稀疏性（负值被置为0，产生稀疏表示）
• 生物学解释：单侧抑制，类似生物神经元的特性

缺点：

• 死亡ReLU问题（某些神经元可能永远不会被激活）
  • 原因：如果学习率太大，权重更新后使神经元仅接收负值输入
  • 解决：使用Leaky ReLU或合适的学习率
• 负值区域完全丢失信息
• 输出不是零中心的

使用场景：

• CNN中最常用的激活函数
• 深度神经网络的默认选择
• 特别适合于深层网络训练

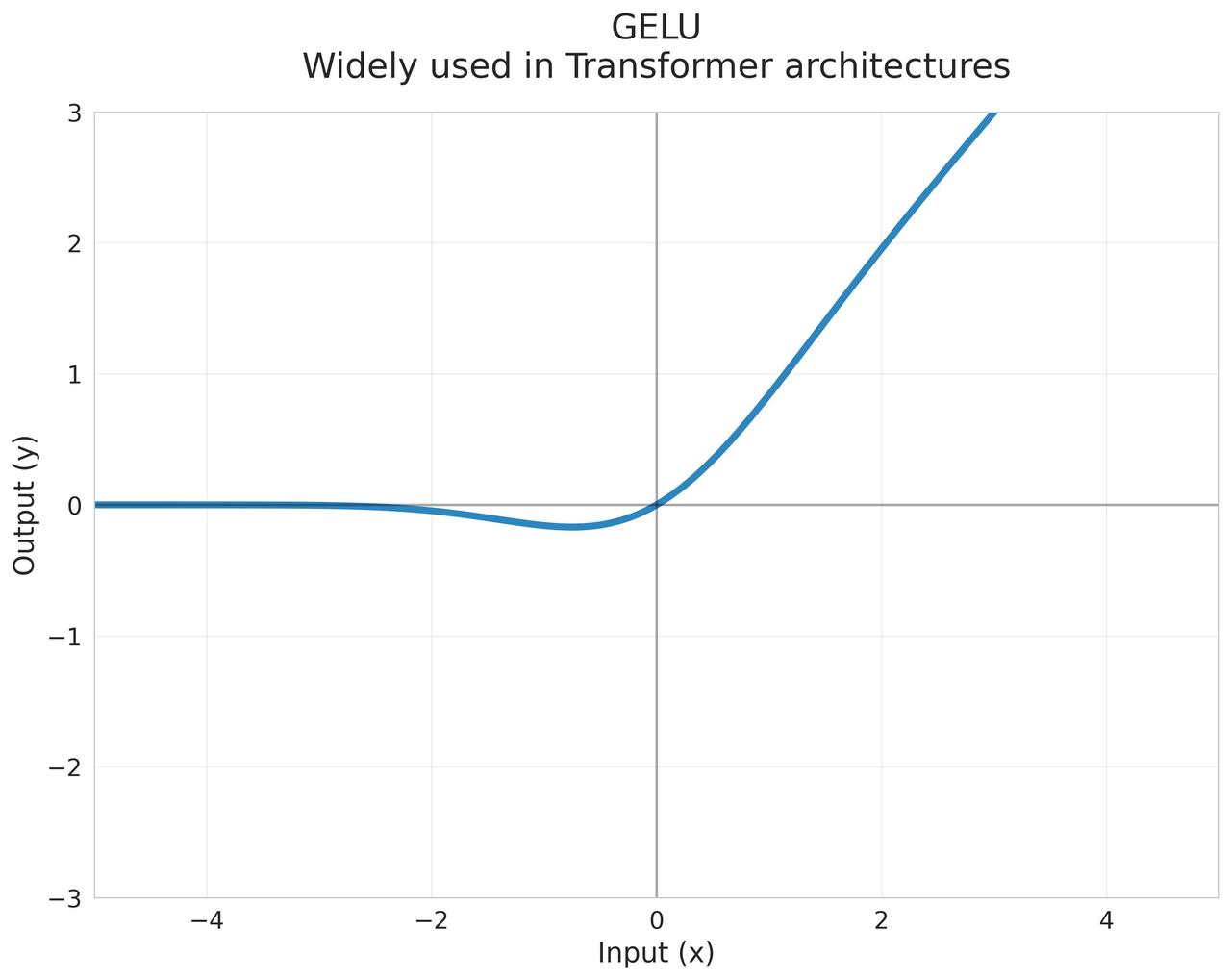
GELU (Gaussian Error Linear Unit)

将输入值乘以来自标准正态分布的概率，是ReLU的平滑版本 $$\text{GELU}(x) = x \cdot \Phi(x) = x \cdot \frac{1}{2}\left[1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right]$$ 其中 $\Phi(x)$ 是标准正态分布的累积分布函数，erf是误差函数

近似计算公式： $$\text{GELU}(x) \approx 0.5x\left(1 + \tanh\left[\sqrt{2/\pi}(x + 0.044715x^3)\right]\right)$$

起源：2016年论文"Gaussian Error Linear Units"提出

优点：

• 在Transformer架构中表现优异
• 平滑激活：在输入的正负区间内都具有平滑性
• 概率解释：可以看作是对输入值的不确定性进行建模，输入值越大，通过的概率越高
• 结合了Dropout的思想，基于概率的软丢弃
• 在x很大时近似于ReLU，很小时近似于线性函数

使用场景：

• Transformer架构的标配（BERT、GPT等都使用GELU）
• 需要平滑非线性的深度学习模型
• 特别适合自然语言处理任务

Sigmoid (Logistic Function)

将输入压缩到(0,1)区间，模拟神经元的开关状态 $$\sigma(x) = \frac{1}{1 + e^{-x}}$$

导数： $$\sigma’(x) = \sigma(x)(1-\sigma(x))$$

起源：最早的激活函数之一，源于生物神经元的激活特性

优点：

• 输出范围固定在(0,1)，适合二分类问题的输出层
• 有明确的概率解释，输出可以表示概率
• 处处可导，导数计算简单
• 具有挤压特性，对异常值不敏感

缺点：

• 存在梯度消失问题
  • 在输入值很大或很小时，梯度接近于0
  • 导数最大值仅为0.25
• 输出不是零中心的，后续层的输入值始终为正
  • 会导致梯度更新的方向偏离最优方向
• 计算复杂度较高，涉及指数运算
• 训练深层网络时收敛较慢

使用场景：

• 二分类问题的输出层
• 门控机制，例如LSTM和GRU的门控单元
• 概率预测任务
• 浅层神经网络

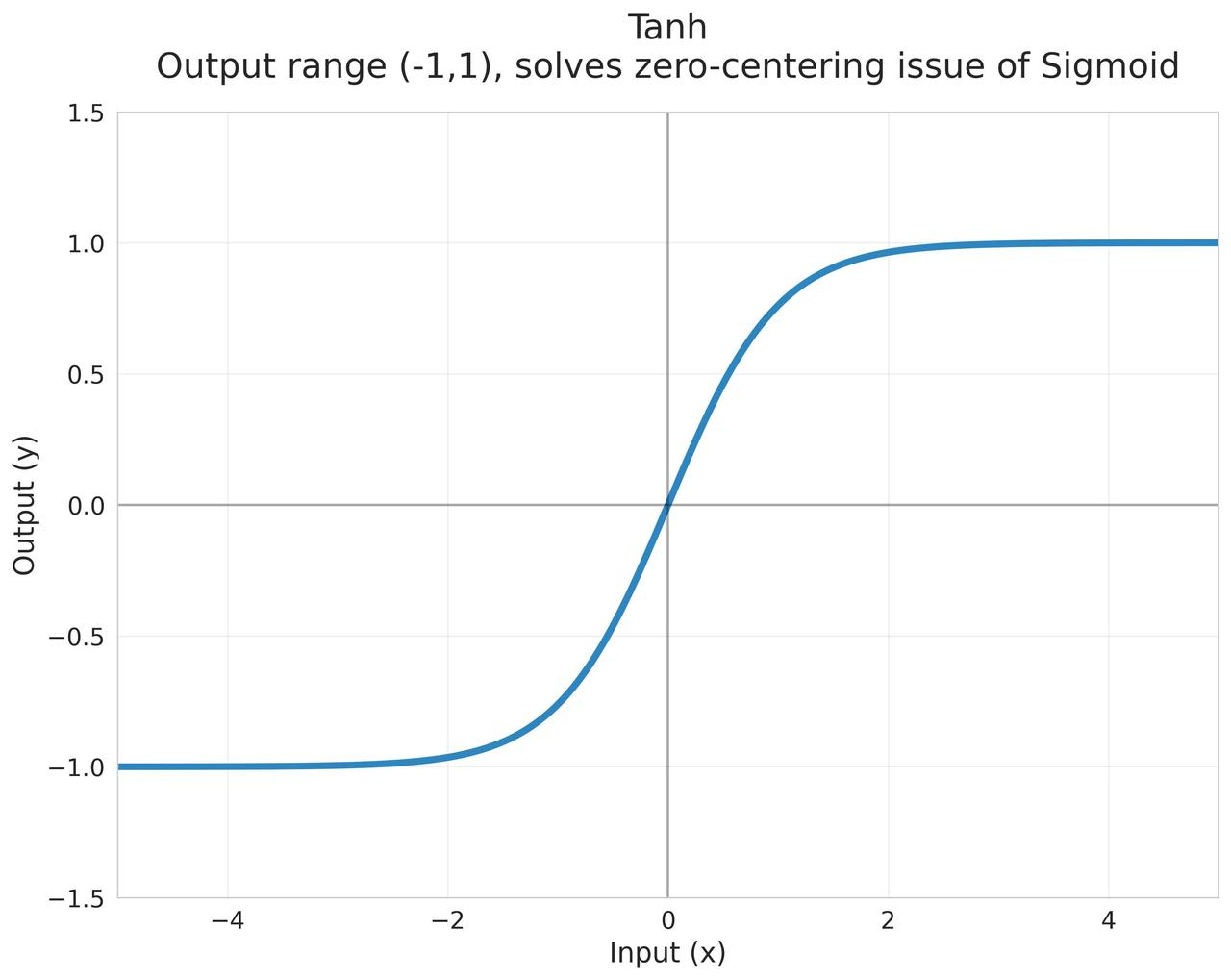
Tanh (Hyperbolic Tangent)

将输入压缩到(-1,1)区间，是Sigmoid的缩放版本 $$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = 2\sigma(2x) - 1$$

导数： $$\tanh’(x) = 1 - \tanh^2(x)$$

起源：Sigmoid的改进版本，1990年代开始广泛使用

优点：

• 输出是零中心的，均值接近0
  • 有助于下一层的学习
  • 使得每一层的输入更加规范化
• 适合处理负值
• 导数比Sigmoid大，训练收敛更快
• 具有挤压特性，可以处理异常值

缺点：

• 仍然存在梯度消失问题
  • 在输入值很大或很小时，梯度接近于0
• 计算复杂度较高，涉及指数运算
• 训练深层网络时仍可能出现收敛慢的问题

使用场景：

• RNN的隐藏层
• 需要零中心化输出的场景
• 需要处理有界输出的场景
• 浅层神经网络

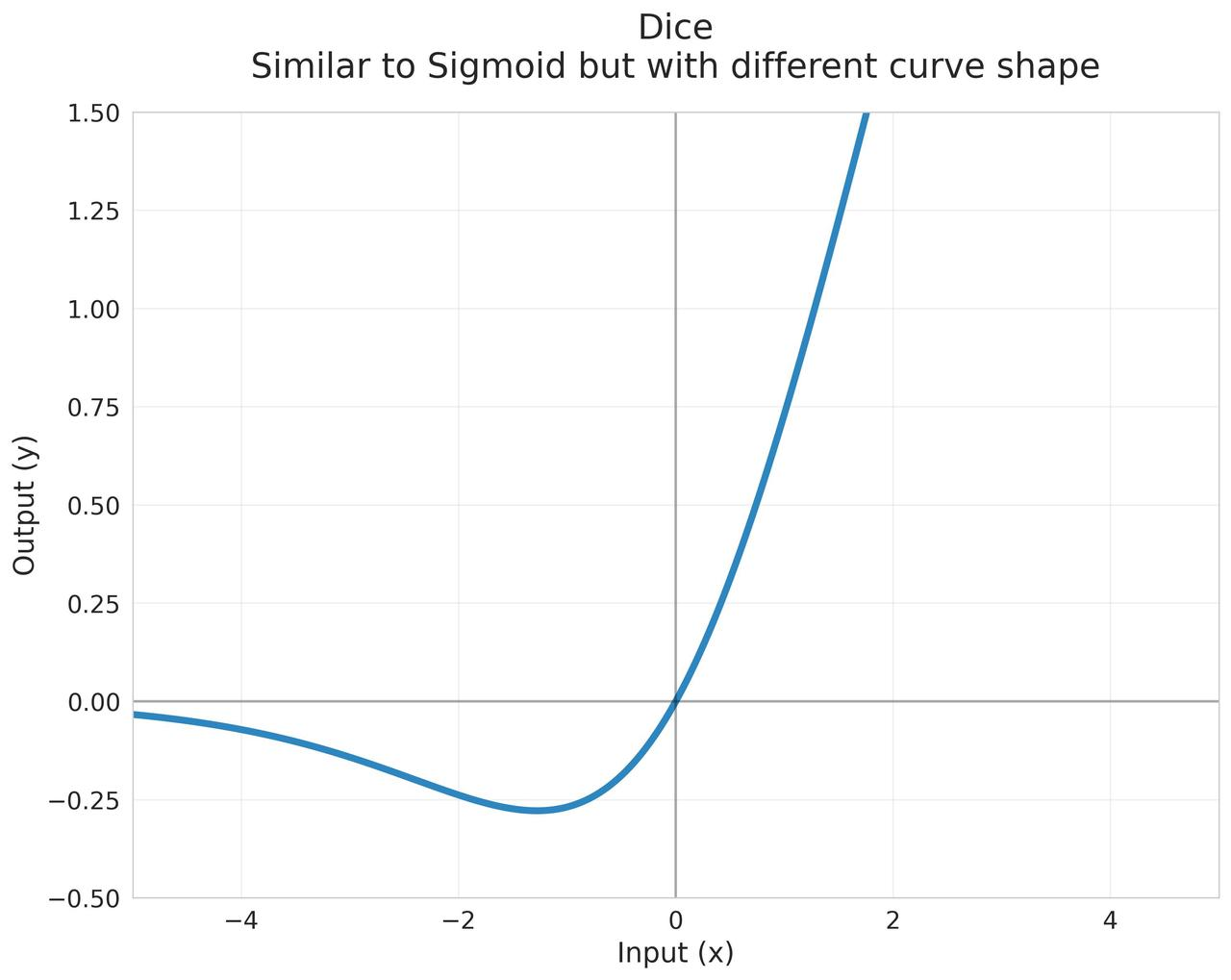
Dice

结合PReLU的自适应特性和Batch Normalization的统计特性，专为稀疏特征设计的激活函数 $$\text{Dice}(x) = x \cdot \sigma(\alpha \cdot (x - \mu))$$ 其中：

• $\sigma$ 是sigmoid函数
• $\alpha$ 是可学习参数
• $\mu$ 是特征的均值（在mini-batch或全局计算）

起源：2018年阿里巴巴在推荐系统中提出

优点：

• 自适应调节
  • 通过引入输入值的均值$μ$和可学习参数$α$
  • 能根据输入数据分布动态调整激活函数形状
  • 在处理不同分布数据时表现更加鲁棒
• 适合处理稀疏特征
  • 对零值或接近零值特征，激活值较小但不会完全置零
  • 保留了稀疏特征中的有用信息
• 结合了归一化的思想
  • 减少了对数据预处理的依赖
• 训练稳定性好
  • 自适应机制减少了过拟合风险

使用场景：

• 推荐系统
• 点击率预测任务
• 处理高度稀疏特征的场景
• CTR/CVR预估模型

Leaky ReLU

给负值区域一个小的斜率，避免完全置零 $$\text{LeakyReLU}(x) = \begin{cases} x & \text{if } x > 0 \ \alpha x & \text{if } x \leq 0 \end{cases}$$ 其中 $\alpha$ 通常是一个很小的正数（如0.01）

起源：2013年为解决ReLU的死亡神经元问题

优点：

• 解决了死亡ReLU问题
  • 负值输入仍然有小的梯度
  • 神经元不会完全停止学习
• 保持了ReLU的其他优点
  • 计算简单
  • 收敛快
• 所有区间都有非零梯度
• 输出均值更接近0

缺点：

• 需要额外设置负值区域的斜率参数
• 性能对斜率参数敏感
• 在实践中效果并不总是优于ReLU

变体：

• PReLU：参数化版本，斜率$\alpha$可学习
• RandomReLU：训练时随机斜率

使用场景：

• 可以作为ReLU的替代品
• 训练不稳定时的首选
• 需要保留负值信息的场景

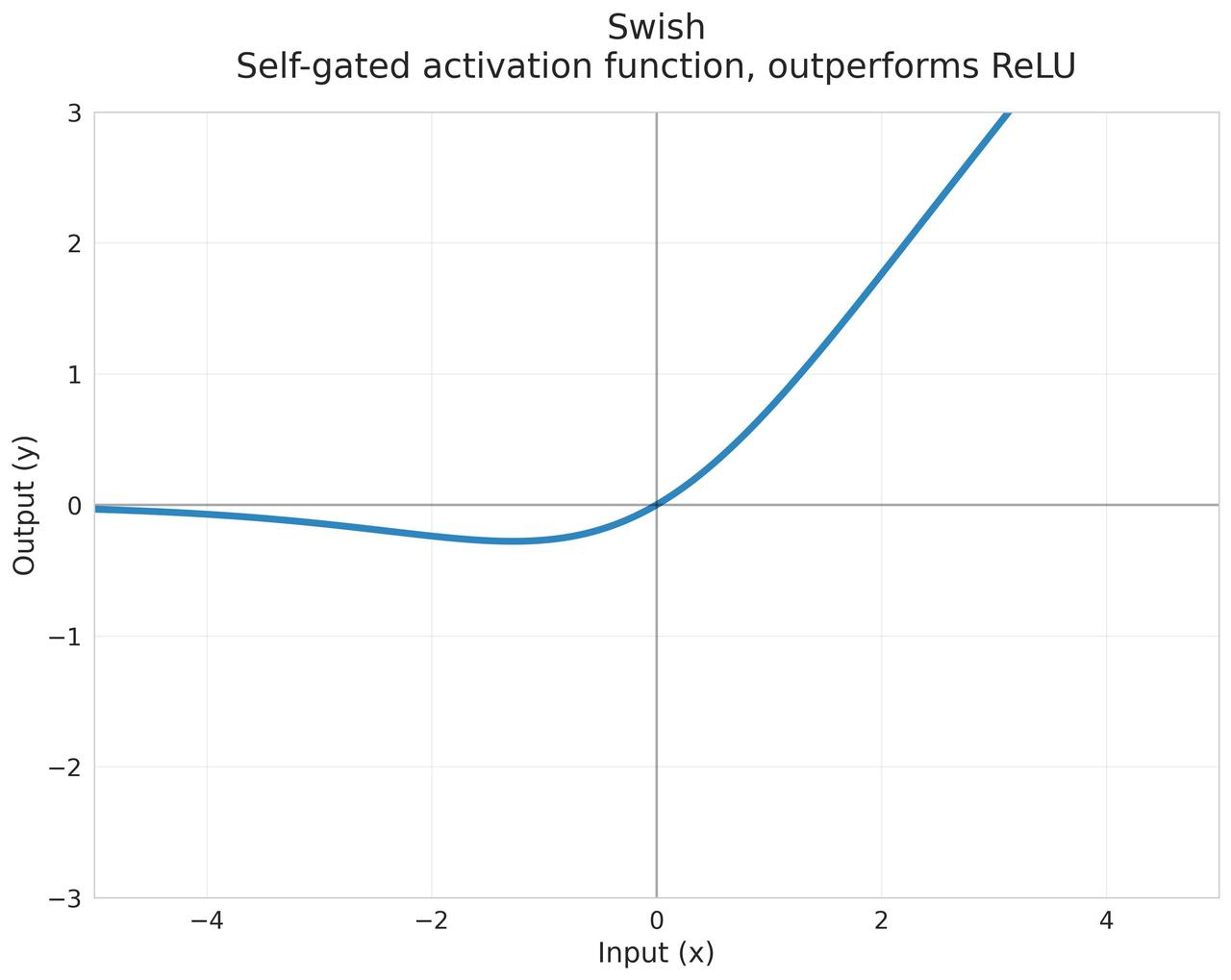
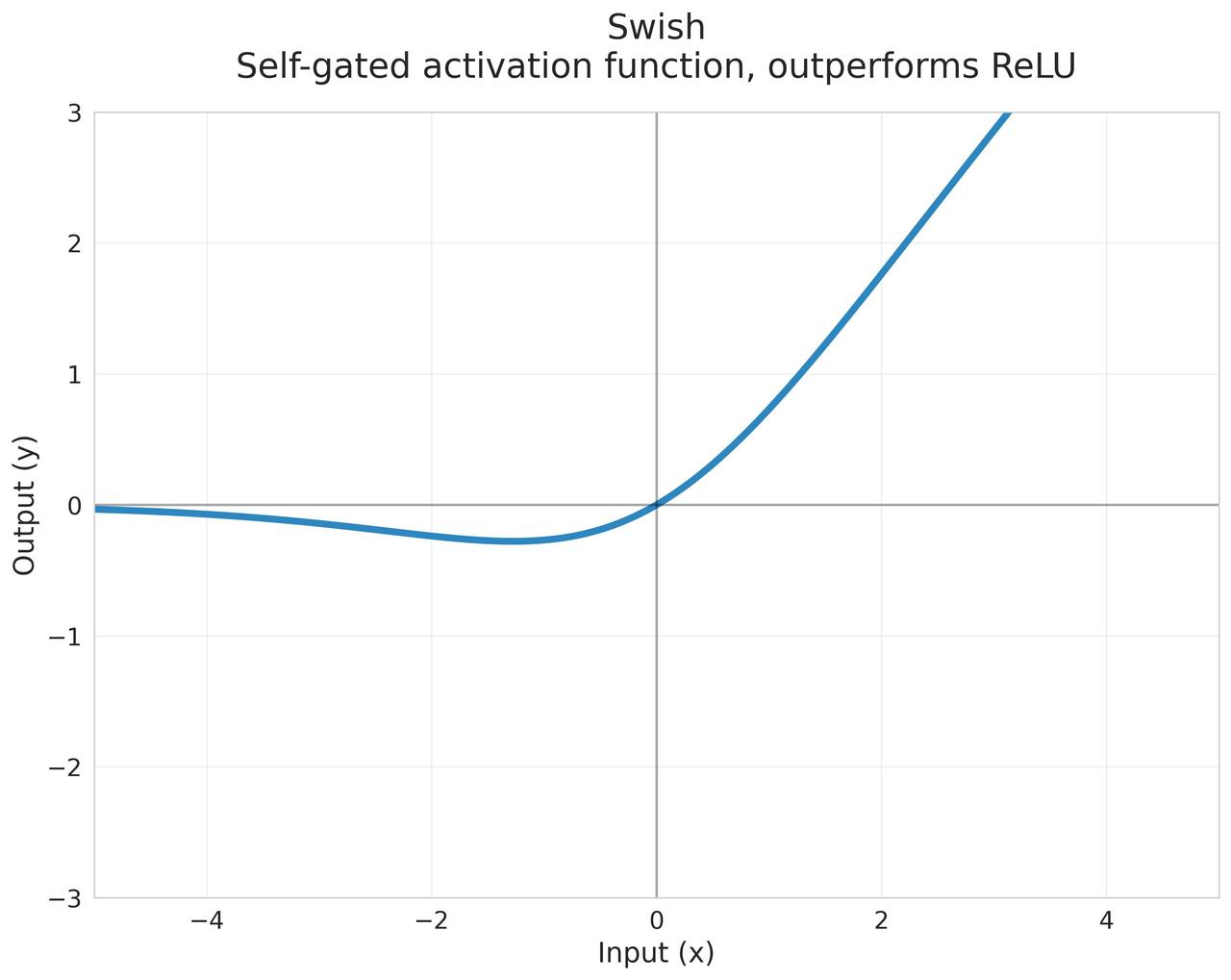
Swish

Google Brain提出的自门控激活函数 $$f(x)=x\cdot\sigma(\beta x)$$ 其中：

• $\sigma$ 是sigmoid函数
• $\beta$ 是可训练参数或固定值

特性：

• 当$\beta \to \infty$时，近似ReLU
• 当$\beta = 0$时，变为线性函数

起源：2017年Google Brain通过神经架构搜索发现

优点：

• 平滑且非单调
  • 有助于优化过程
  • 可能捕获更复杂的模式
• 在深层网络中表现优于ReLU
• 无需人工设置参数（$\beta$可学习）
• 计算效率高
• 具有有界梯度

缺点：

• 计算量比ReLU大
• 需要存储额外的激活值
• 在某些任务上提升不明显

使用场景：

• 深层神经网络
• 计算机视觉任务
• 可作为ReLU的直接替代品

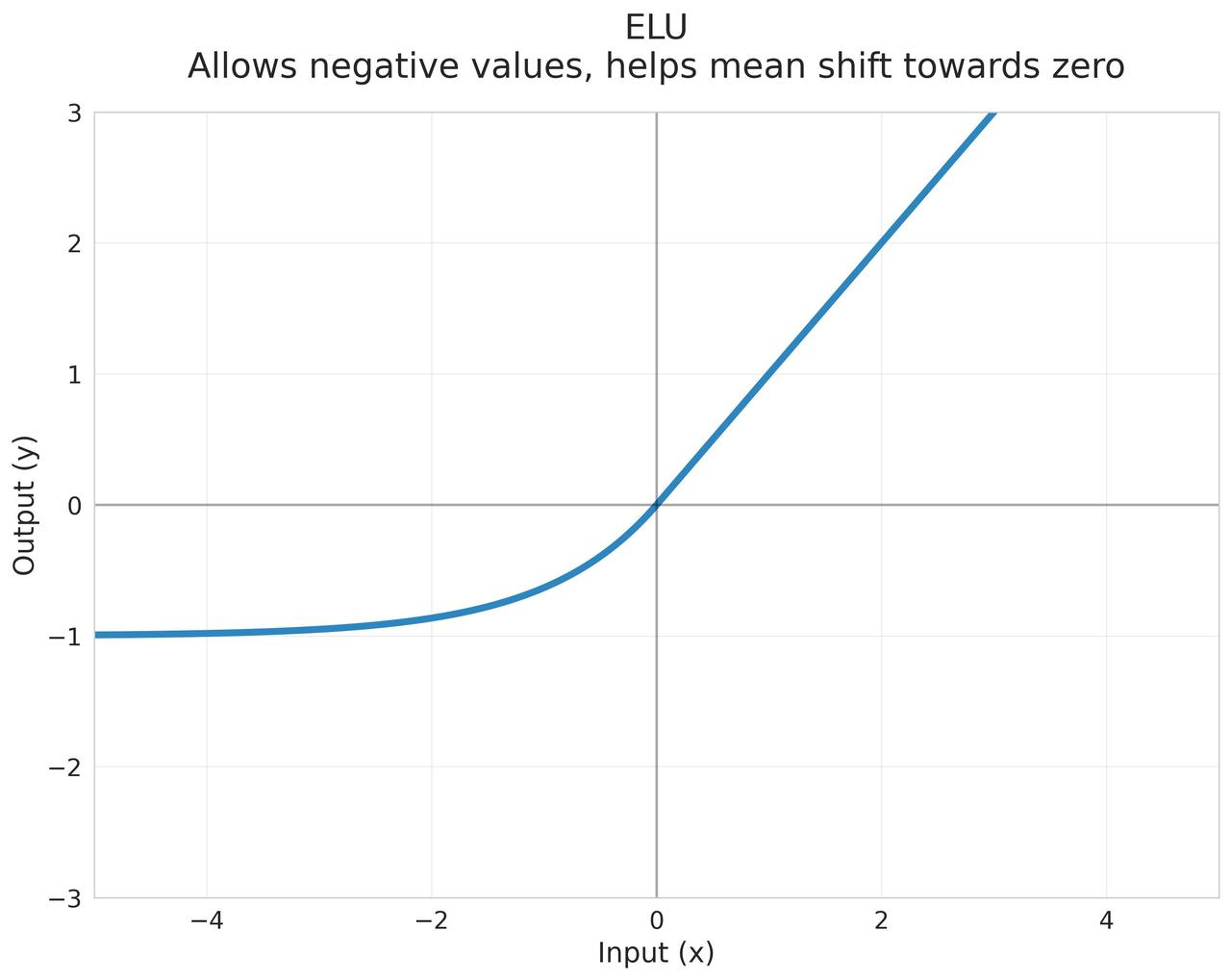
ELU (Exponential Linear Unit)

负值区域使用指数函数，使均值更接近零 $$\text{ELU}(x) = \begin{cases} x & \text{if } x > 0 \ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}$$ 其中 $\alpha$ 是一个正常数（通常为1）

起源：2015年论文"Fast and Accurate Deep Network Learning by Exponential Linear Units"

优点：

• 可以缓解偏移现象
  • 负值的均值接近0
  • 减少了偏置偏移
• 对噪声更鲁棒
  • 负值区域的饱和性质有助于抑制噪声
• 在零点附近有平滑的导数
• 自归一化特性
• 能产生负值输出，增加表达能力

缺点：

• 计算复杂度比ReLU高
• 需要额外的指数运算
• $\alpha$参数需要预先设定

使用场景：

• 需要处理噪声数据的深度学习任务
• 对数据分布敏感的任务
• 需要负值激活的场景

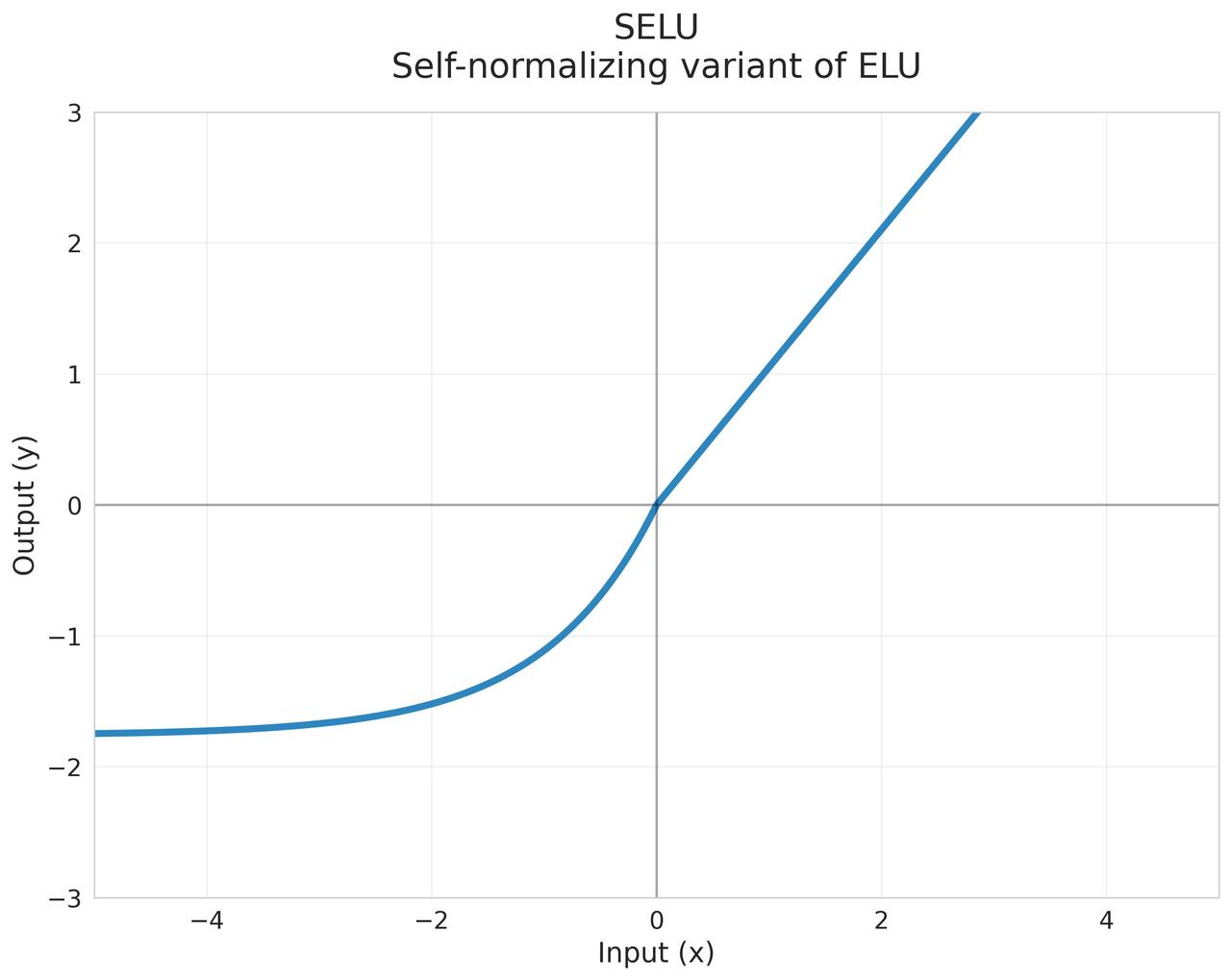
SELU (Scaled Exponential Linear Unit)

通过精心设计的缩放因子实现自归一化 $$\text{SELU}(x) = \lambda \begin{cases} x & \text{if } x > 0 \ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}$$ 其中：

• $\lambda \approx 1.0507$
• $\alpha \approx 1.6733$

这两个参数是精心计算的固定值，用于保证自归一化性质

起源：2017年论文"Self-Normalizing Neural Networks"

优点：

• 自归一化特性
  • 自动保持均值和方差稳定
  • 不需要额外的批归一化层
• 训练更稳定
• 更强的正则化效果
• 适合深层网络

注意事项：

• 需要特定的权重初始化（LeCun正态初始化）
• 输入需要标准化
• 不适合CNN等结构

使用场景：

• 全连接网络
• 需要自归一化的场景
• 深层前馈网络

Mish

平滑的非单调激活函数 $$\text{Mish}(x) = x \cdot \tanh(\ln(1 + e^x))$$

导数： $$\text{Mish}’(x) = \frac{e^x(\omega + 1 + e^x\omega)}{(1 + e^x)^2}$$ 其中 $\omega = \tanh(\ln(1 + e^x))$

起源：2019年论文"Mish: A Self Regularized Non-Monotonic Neural Activation Function"

优点：

• 无上界有下界
  • 上界无限制
  • 下界约为-0.31
• 平滑度高
  • 所有阶导数连续
  • 有助于优化
• 在多个基准测试中表现优异
• 保留了更多梯度信息
• 自正则化特性

缺点：

• 计算开销大
• 内存使用较多
• 训练时间可能增加

使用场景：

• 计算机视觉任务
• 深度神经网络
• 需要强大表达能力的模型
• 可作为ReLU的替代品