在传统的深度神经网络(尤其是残差网络,ResNet)中,每一层的残差块(Residual Block)都会对输入进行处理,然后将结果与输入相加,形成输出。这种结构虽然有效,但在某些情况下,部分残差块可能对某些特定输入并不重要,直接跳过它们可以减少计算量,同时保持模型性能。
序列模型叠叠乐有收益
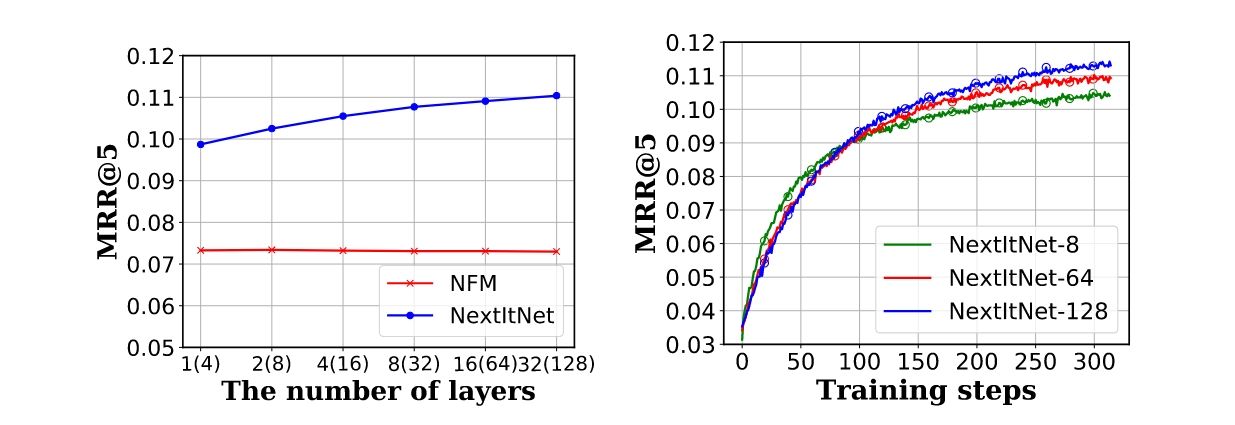
NFM叠叠乐没有收益,但是NextItNet叠叠乐有收益,在128层的时候取得最好结果
As shown, on (a), we clearly observe that NFM yields no accuracy gain by deepening the number of network layers, and it performs largely worse than NextItNet. In contrast, the performance of NextItNet is gradually improved by stacking more layers. To our surprise, NextItNet converges the best with up to 128 layer, achieving around 1% improvement on MRR@5 over the same model with 64 layers, as shown in (b).
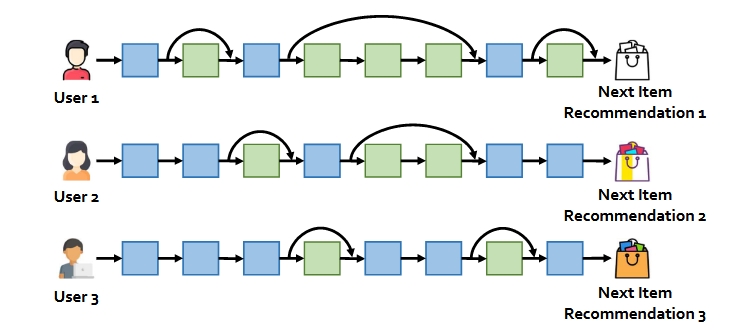
SkipRec,自动跳过一些层
SkipRec是一个通用的网络深度选择框架,一个用于深度顺序推荐模型的自适应推理框架,它在每个用户的基础上自适应地定义网络结构。具体来说,我们设计了一个策略网络来自动确定骨干网中的哪些层应该保留,哪些层应该跳过,从而在SRS中获得用户特定的决策。
值得注意的是,SkipRec是模型不可知的,并且可能适用于任何具有深度网络架构的SR模型。具体来说,SkipRec由两个主要模块组成:骨干网和策略网。骨干网是稍加修改的NextItNet模型(稍后描述),比原始版本更强大。我们设计了一个策略网络,以每个用户为基础自动确定骨干网中哪些层应该保留,哪些层应该跳过,从而真正实现用户特定的决策。
策略网络
-
策略网络: 策略网络会根据当前输入的用户序列 $E_u$,生成一个二元策略 $I_l(E_u)$,用于决定第 $l$ 个残差块是否被跳过。
- $I_l(E_u) = 1$:保留第 $l$ 个残差块。
- $I_l(E_u) = 0$:跳过第 $l$ 个残差块,直接使用上一层的输出。
-
自适应输出: 第 $l$ 个残差块的输出 $E_u^{l \text{ adaptive}}$ 是根据策略 $I_l(E_u)$ 动态计算的,计算公式为: $$ E_u^{l \text{ adaptive}} = I_l(E_u) E_u^l + (1 - I_l(E_u)) E_u^{l-1 \text{ adaptive}} $$ 其中:
- $E_u^l$:第 $l$ 个残差块的输出。
- $E_u^{l-1 \text{ adaptive}}$:上一层的自适应输出。
如果 $I_l(E_u) = 1$,则 $E_u^{l \text{ adaptive}} = E_u^l$,即保留当前残差块的输出; 如果 $I_l(E_u) = 0$,则 $E_u^{l \text{ adaptive}} = E_u^{l-1 \text{ adaptive}}$,即跳过当前残差块,直接使用上一层的输出。
-
策略的生成: 策略 $I_l(E_u)$ 是基于用户序列 $E_u$ 通过一个小型策略网络生成的概率分布中采样的结果。这个分布是一个二元分布,表示“保留”或“跳过”残差块的概率。

Gumbel Softmax Sampling
在许多机器学习任务中,我们需要从离散分布中采样,例如在 SkipRec 模型中,我们需要根据策略网络输出的概率分布决定是否“保留”或“跳过”某个残差块。然而,直接从离散分布中采样是不可微分的,这会导致无法通过梯度下降法优化模型。
Gumbel Softmax Sampling 通过引入 Gumbel 分布 和 Softmax 松弛,使得从离散分布中采样变得可微分,从而解决了这一问题。这个机制使得策略网络可以与骨干网络联合优化,从而实现端到端的训练。
核心思想
Gumbel Softmax Sampling 的核心思想是:
- 使用 Gumbel 分布 为每个类别的 logits(对数概率)添加噪声,从而引入随机性。
- 使用 Softmax 函数 对加噪后的 logits 进行连续松弛,从而使得采样过程可微分。
Gumbel 分布
Gumbel 分布是一种极值分布,常用于模拟最大值或最小值的分布。其概率密度函数为: $$ f(x) = e^{-(x + e^{-x})} $$ Gumbel 分布的一个重要性质是:如果 $g_1, g_2, \ldots, g_k$ 是从 Gumbel(0, 1) 分布中独立采样的随机变量,那么: $$ \arg\max_i (\log \pi_i + g_i) $$ 服从类别概率为 $\pi_i$ 的离散分布。这一性质是 Gumbel Softmax Sampling 的基础。
Gumbel Softmax Sampling 步骤
假设我们有 $k$ 个类别,每个类别的概率为 $\pi_1, \pi_2, \ldots, \pi_k$。Gumbel Softmax Sampling 的步骤如下:
采样 Gumbel 噪声
从 Gumbel(0, 1) 分布中采样 $k$ 个独立随机变量 $g_1, g_2, \ldots, g_k$。具体采样方法为: $$ g_i = -\log(-\log(u_i)) $$ 其中 $u_i \sim \text{Uniform}(0, 1)$。
加噪并计算 Softmax
对每个类别的 logits 加上 Gumbel 噪声,然后通过 Softmax 函数计算连续松弛的输出: $$ \alpha_i = \frac{\exp((\log \pi_i + g_i) / \tau)}{\sum_{j=1}^k \exp((\log \pi_j + g_j) / \tau)} $$ 其中 $\tau$ 是温度参数,用于控制输出的离散程度。当 $\tau \to 0$ 时,$\alpha$ 接近于 one-hot 向量;当 $\tau \to \infty$ 时,$\alpha$ 接近于均匀分布。
采样与松弛
在 前向传播 时,直接使用 $\arg\max$ 操作从离散分布中采样(硬采样): $$ z = \text{one-hot}\left(\arg\max_i (\log \pi_i + g_i)\right) $$ 在 反向传播 时,使用 Softmax 松弛后的 $\alpha$ 计算梯度,从而使得整个过程可微分。
在 SkipRec 中的应用
在 SkipRec 模型中,策略网络输出每个残差块的“保留”或“跳过”概率 $\pi_1$ 和 $\pi_2$(其中 $\pi_1 + \pi_2 = 1$)。Gumbel Softmax Sampling 被用于从这两个概率中采样动作 $z$: $$ z = \text{one-hot}\left(\arg\max_i (\log \pi_i + g_i)\right) $$ 具体步骤为:
- 从 Gumbel(0, 1) 分布中采样 $g_1$ 和 $g_2$。
- 计算加噪后的 logits:$\log \pi_1 + g_1$ 和 $\log \pi_2 + g_2$。
- 使用 $\arg\max$ 选择动作 $z$(“保留”或“跳过”)。
- 在前向传播中使用 $z$ 决定是否跳过残差块。
- 在反向传播时,使用 Gumbel Softmax 松弛(公式 7)计算梯度,从而优化策略网络。
温度参数 $\tau$ 的作用
温度参数 $\tau$ 控制了采样输出的离散程度:
- 当 $\tau \to 0$ 时,$\alpha$ 接近于 one-hot 向量,采样结果更接近于硬采样。
- 当 $\tau \to \infty$ 时,$\alpha$ 接近于均匀分布,采样结果更平滑。
在 SkipRec 中,默认设置 $\tau = 10$,以平衡离散性和可微性。
