CF发展史：从无邻居到多跳邻居

CF（协同过滤）的发展历程可以看作是从无邻居到多跳邻居的逐步深化过程，充分利用了用户-物品互动图中的结构信息。以下是这一发展路径的简要梳理：

无邻居信息：矩阵分解（Matrix Factorization, MF）

矩阵分解是早期CF的基础方法，它将用户和物品分别映射到低维潜在空间中，通过内积预测用户对物品的兴趣 。此时，模型仅依赖用户的单一ID作为输入，未显式利用用户的历史互动信息，相当于无邻居信息的简化模型。

引入一跳邻居：SVD++ 和 NAIS

随着研究深入，发现用户的历史互动信息（即用户的一跳邻居）对提升预测性能至关重要。

• SVD++ 将用户的历史评分物品作为额外特征，融入矩阵分解框架中，显著提升了评分预测的准确性。
• NAIS（Neural Attentive Item Similarity） 进一步通过注意力机制区分用户历史互动中不同物品的重要性，优化了物品排序预测。

这一阶段的改进可以看作是从无邻居信息到利用一跳邻居的演进。

引入多跳邻居：NGCF 和 LightGCN

为了进一步利用用户-物品互动图中的高阶结构信息，研究者开始探索多跳邻居的作用。

• NGCF（Neural Graph Collaborative Filtering） 首次将图卷积网络（GCN）引入CF任务，通过多层消息传播（即多跳邻居）来优化用户和物品的嵌入表示。虽然NGCF取得了显著性能提升，但其设计较为复杂，直接继承了GCN的特征变换和非线性激活操作，这些操作对CF任务并非必要，甚至可能带来负面影响。
• LightGCN 在NGCF的基础上进行了简化，仅保留了GCN中邻居聚合这一核心操作，通过更高效的多跳邻居信息传播机制，进一步提升了模型性能，同时降低了训练复杂度。

这一阶段标志着CF从一跳邻居发展到多跳邻居，并逐渐优化了多跳信息利用的方式。

基于NGCF的实证实验

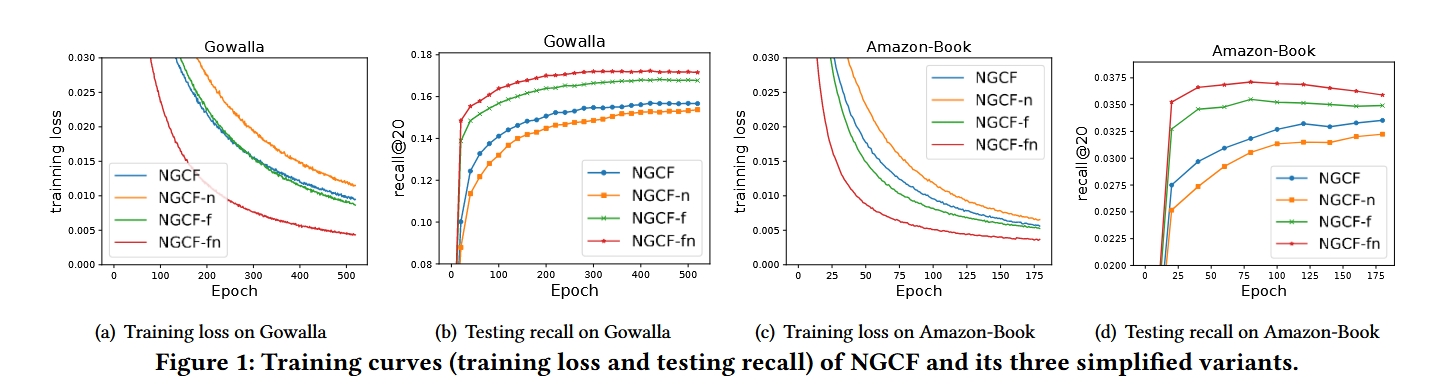
1. 特征变换对NGCF的负面影响
   • 结论：在NGCF和NGCF-n模型中，移除特征变换操作显著提升了模型性能。
   • 解读：特征变换是图卷积网络（GCN）中的核心操作之一，通常用于对节点特征进行非线性映射。然而，在CF任务中，用户和物品节点仅由其ID表示，缺乏语义信息。在这种情况下，对ID嵌入进行多次非线性特征变换并不会带来有益的表示能力，反而增加了模型复杂度，导致性能下降。因此，特征变换对NGCF的任务效果产生了负面影响。
2. 非线性激活的影响
   • 当特征变换存在时：非线性激活对模型性能的影响较小，但仍未带来明显的性能提升。
   • 当特征变换移除时：非线性激活的影响更加显著，且表现为负面影响。
   • 解读：非线性激活通常用于增强模型的表达能力，但在CF任务中，由于用户和物品的嵌入表示较为简单（仅基于ID），引入额外的非线性操作并未有效提升模型的学习能力，反而可能干扰嵌入的优化过程。
3. 特征变换与非线性激活的综合影响
   • 结论：在同时移除特征变换和非线性激活的情况下，NGCF-fn 模型相比NGCF取得了显著性能提升（召回率相对提升9.57%）。
   • 解读：特征变换和非线性激活作为GCN中的标准操作，虽然在节点分类等任务中表现优异，但在CF任务中并不适用。移除这两个操作不仅简化了模型设计，还显著提升了性能，证明了它们对NGCF的任务效果具有较大的负面影响。

图卷积视角下的LightGCN

GCN的基本思想

图卷积网络（GCN）的核心思想是通过在图结构上平滑节点特征来学习节点表示。为实现这一目标，GCN通过迭代执行图卷积操作，即聚合邻居节点的特征作为目标节点的新的表示。这种邻域聚合可以抽象为以下形式： $$ e_u^{(k+1)} = \text{AGG}\left(e_u^{(k)}, {e_i^{(k)} : i \in N_u}\right), $$ 其中，AGG 是一个聚合函数，它考虑了目标节点及其邻居节点在第 k 层的表示。聚合函数是图卷积的核心，其设计直接影响模型的表达能力。

现有聚合函数的设计

许多研究提出了不同的聚合函数设计：

• GIN：采用加权求和聚合器，强调邻居特征的线性组合。
• GraphSAGE ：使用LSTM聚合器，引入序列建模能力。
• BGNN：提出双线性交互聚合器，捕捉邻居与目标节点之间的高阶关系。

然而，这些方法通常将特征变换或非线性激活与聚合函数紧密结合。尽管这种设计在节点分类或图分类任务中表现良好（尤其是在输入特征具有语义信息时），但在协同过滤（CF）任务中，这种复杂性可能会成为负担。

LightGCN的简化设计

在LightGCN中，我们从图卷积视角出发，对聚合函数进行了以下两方面的简化：

聚合上的简化

LightGCN摒弃了特征变换和非线性激活，仅保留最简单的加权求和聚合器： $$ e_u^{(k+1)} = \sum_{i \in N_u} \frac{1}{\sqrt{|N_u|} \sqrt{|N_i|}} e_i^{(k)}. $$ 这种设计的核心思想是：在CF任务中，节点特征仅为ID信息，复杂的特征变换和非线性激活不仅无法提升性能，反而可能引入噪声，降低模型表现。通过简化聚合函数，LightGCN能够更高效地捕捉用户与物品之间的协同信号。

无需显式自连接

传统GCN通常需要显式地将目标节点的自连接纳入聚合过程，以确保聚合后的表示能够保留目标节点自身的信息。然而，在LightGCN中，我们通过层组合（Layer Combination）机制自然地引入自连接，因此无需在每一层的聚合中显式地处理自连接问题。具体来说，LightGCN最终的用户和物品表示为所有层嵌入的加权和，如下： $$ e_u = \sum_{k=0}^K \alpha_k e_u^{(k)}, \quad e_i = \sum_{k=0}^K \alpha_k e_i^{(k)}, $$ 其中，e_u^(k) 和 e_i^(k) 分别表示用户 u 和物品 i 在第 k 层的嵌入，α_k 为层权重。由于第 0 层的嵌入 e_u⁽⁰⁾ 和 e_i⁽⁰⁾ 直接表示目标节点自身的初始表示，这种层组合机制实际上已经隐式地包含了自连接的效果。

矩阵视角下的LightGCN

为了便于实现以及与现有模型的比较，我们给出了LightGCN的矩阵形式。

用户-物品交互矩阵与邻接矩阵

设用户-物品交互矩阵为 R ∈ ℝ^M×N，其中 M 和 N 分别表示用户和物品的数量。矩阵中的每个元素 R_ui = 1 表示用户 u 与物品 i 存在交互，否则为 0。基于此，用户-物品图的邻接矩阵 A 可以表示为： $$ A = \begin{bmatrix} 0 & R \\ R^T & 0 \end{bmatrix}, $$ 这里 A 是一个 (M + N) × (M + N) 的矩阵，用户和物品节点共同构成了图的节点集合。

LightGCN的矩阵形式

设第 0 层嵌入矩阵为 E⁽⁰⁾ ∈ ℝ^{(M + N) × T}，其中 T 为嵌入维度。LightGCN中图卷积的矩阵形式可以表示为： $$ E^{(k+1)} = \left(D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\right) E^{(k)}, $$ 其中 D 是一个 (M + N) × (M + N) 的对角矩阵，其每个元素 D_ii 表示邻接矩阵 A 第 i 行向量中非零元素的个数（也称为度矩阵）。矩阵 D^-½ A D^-½ 是对邻接矩阵 A 进行对称归一化后的矩阵。

最终嵌入矩阵与模型预测

在LightGCN中，最终嵌入矩阵通过各层嵌入的加权求和得到： $$ E = \alpha_0 E^{(0)} + \alpha_1 E^{(1)} + \alpha_2 E^{(2)} + \dots + \alpha_K E^{(K)} $$ 其中 α₀, α₁, …, α_K 是各层嵌入的权重 将其表示为矩阵形式： $$ E = \alpha_0 E^{(0)} + \alpha_1 \tilde{A} E^{(0)} + \alpha_2 \tilde{A}^2 E^{(0)} + \dots + \alpha_K \tilde{A}^K E^{(0)} $$ 其中 $\tilde{A} = D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$ 是归一化后的邻接矩阵

LightGCN的层组合机制

背景与动机

在LightGCN中，第0层的嵌入（即用户和物品的初始嵌入）是唯一需要学习的模型参数。通过多层图卷积（LGC），我们可以得到每一层的嵌入。为了生成最终的表示，LightGCN采用了一种层组合（Layer Combination）机制，将每一层的嵌入加权求和。这种设计有三方面的动机：

1. 防止过度平滑（Over-smoothing）：随着层数的增加，节点嵌入会逐渐趋于相似，导致信息丢失。
2. 捕捉不同层次的语义：每一层的嵌入捕捉了不同阶次的邻近关系（如直接交互、跨用户/物品的交互等）。
3. 隐式引入自连接：通过层组合机制，可以自然地实现自连接的效果，无需在每层中显式处理。

层组合的定义

在K层图卷积之后，LightGCN将各层的嵌入加权求和，生成用户和物品的最终表示： $$ e_u = \sum_{k=0}^K \alpha_k e_u^{(k)}, \quad e_i = \sum_{k=0}^K \alpha_k e_i^{(k)}, $$ 其中：

• e_u^(k) 和 e_i^(k) 分别表示用户 u 和物品 i 在第 k 层的嵌入。
• α_k 是第 k 层嵌入的权重，用于控制不同层嵌入的重要性。

权重的设置

α_k 可以通过以下两种方式确定：

1. 作为超参数手动调整：例如，将 α_k 均匀设置为 1/(K+1)。
2. 作为模型参数自动优化：例如，通过注意力网络学习权重。

在LightGCN中，为了保持模型的简洁性，默认将 α_k 均匀设置为 1/(K+1)。实验表明，这种简单的设置已经能够取得良好的性能。

层组合的优势

层组合机制的优势主要体现在以下三个方面：

防止过度平滑

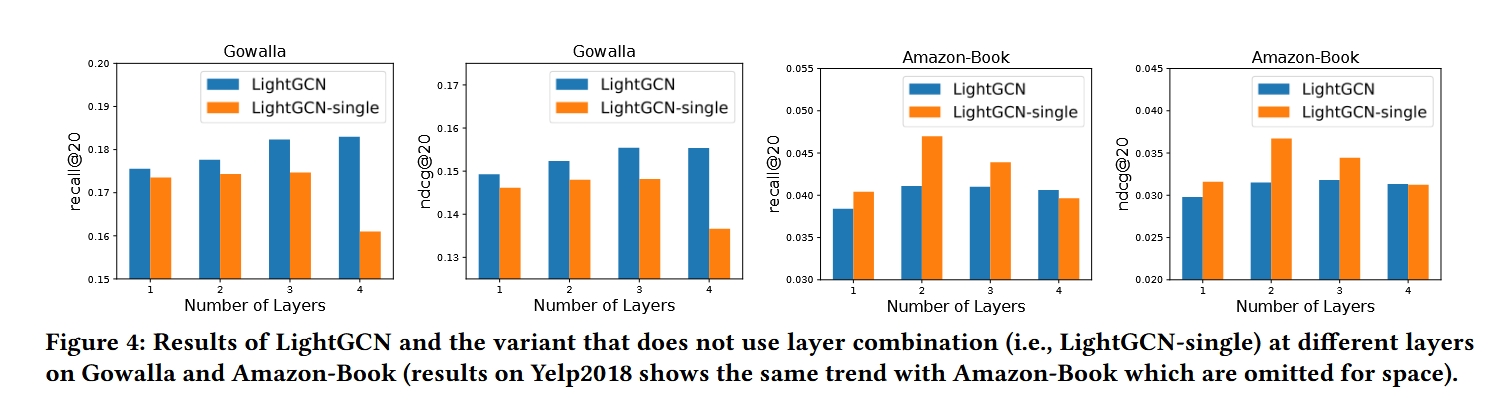
随着层数的增加，节点嵌入会逐渐趋于相似，这种现象称为过度平滑 。如果仅使用最后一层的嵌入，可能会导致信息丢失。通过组合各层嵌入，可以缓解这一问题。

下图中LightGCN-single就是使用最后一层的结果

捕捉不同层次的语义

每一层的嵌入捕捉了不同阶次的邻近关系：

• 第0层：保留节点自身信息，实现隐式自连接。
• 第1层：对直接交互的用户和物品进行平滑。
• 第2层：对共享交互项的用户或共享用户的物品进行平滑。
• 更高层：捕捉更高阶的邻近关系 。

通过组合各层嵌入，可以使最终的表示更加全面，捕捉到不同层次的语义信息。

隐式引入自连接

在图卷积中，自连接是一个重要的技巧，用于在聚合邻居信息的同时保留目标节点自身的特征。在LightGCN中，层组合机制通过加权求和的方式自然地引入了自连接的效果，无需在每一层中显式处理。具体来说，第 0 层的嵌入 e_u⁽⁰⁾ 和 e_i⁽⁰⁾ 直接表示目标节点自身的初始表示，因此在最终的加权和中，目标节点自身的特征已经被包含。关于这一点，可以参考第3.2.1节的证明。

模型预测

在获得用户和物品的最终表示后，LightGCN通过内积计算预测分数： $$ \hat{y}_{ui} = e_u^\top e_i, $$ 其中，$\hat{y}_{ui}$ 是用户 u 对物品 i 的预测分数，用于生成推荐列表。