Faiss，脸书开源的向量数据库

Faiss 参数总结

Faiss（Facebook AI Similarity Search）是一个高效的高维向量相似性搜索库，广泛应用于大规模相似性检索任务。以下是Faiss中关键参数的总结与解析：

`dim`（向量维数）

含义：向量的维度。
作用：指定输入向量的维度，Faiss会根据维度初始化索引结构。
示例：对于128维的特征向量，dim为128。

`param`（索引参数）

含义：用于指定需要构建的索引类型。
作用：Faiss支持多种索引类型，param参数用于选择具体的索引类型和配置。
常用索引类型:
- FlatIndex：暴力搜索（精确检索）。
- IVFFlat：倒排索引结合暴力搜索，适合大规模数据。
- HNSW：基于分层导航小世界图的近似最近邻搜索。
- IVFPQ：倒排索引结合乘积量化，适合高维大规模数据。
- LSH：局部敏感哈希，适合低维数据。
- ScalarQuantizer：标量量化索引。
示例：param = "Flat"表示选择暴力搜索索引。

`measure`（度量方法）

含义：用于指定向量相似性计算的方法。
作用：度量方法决定了向量之间的距离或相似性如何计算。
支持的度量方法：
- METRIC_INNER_PRODUCT：内积（用于计算余弦相似度，需先将向量归一化）。
- METRIC_L1：曼哈顿距离（L1距离）。
- METRIC_L2：欧氏距离（L2距离）。
- METRIC_Linf：无穷范数（最大绝对值距离）。
- METRIC_Lp：p范数（p值可自定义，如L3、L4等）。
- METRIC_BrayCurtis：Bray-Curtis相异度（常用于生态学数据）。
- METRIC_Canberra：堪培拉距离（适用于稀疏数据）。
- METRIC_JensenShannon：JS散度（用于概率分布之间的距离）。

索引构建与检索的常见流程

初始化索引：

1
2
3


import faiss
dim = 128  # 向量维度
index = faiss.IndexFlatL2(dim)  # 使用L2距离的Flat索引

添加数据：

1
2


vectors = ...  # 待添加的向量数据
index.add(vectors)  # 将数据添加到索引中

检索相似向量：

1
2
3


query_vector = ...  # 查询向量
k = 10  # 返回最近邻的数量
distances, indices = index.search(query_vector, k)  # 检索

Flat ：暴力检索

优点：该方法是Faiss所有index中最准确的，召回率最高的方法，没有之一
缺点：速度慢，占内存大
适用情况：向量候选集很少，在50万以内，并且内存不紧张
是否支持GPU：支持GpuIndexFlat
是否需要训练：不需要
工程优化：虽然都是暴力检索，faiss的暴力检索速度比一般程序猿自己写的暴力检索要快上不少

1
2
3
4
5


dim, measure = 64, faiss.METRIC_L2
param = 'Flat'
index = faiss.index_factory(dim, param, measure)
index.is_trained                                   # 输出为True
index.add(xb)                                      # 向index中添加向量

IVFx Flat ：倒排暴力检索

文档倒排索引：在文档检索场景中，
- 倒排索引的核心思想是将关键词（keyword）与包含该关键词的文档（document）建立映射关系
- 由于关键词的数量远远小于文档数量，这种索引方式能够显著减少检索时间
向量倒排索引：在向量检索中，IVF 也采用了类似的思想：
- 通过 k-means 聚类，将所有向量划分到不同的聚类中心（cluster center）下
- 每个聚类中心作为一个“关键词”，挂上属于该中心的向量列表（非中心向量）
- 查询时，首先找到与查询向量最近的几个聚类中心，然后在这些中心下的向量列表中进行精确搜索
优点：IVFx 通过缩小搜索范围（仅搜索最近的聚类中心下的向量），IVF 显著提升了检索效率
缺点：速度也还不是很快
参数：IVFx中的x是k-means聚类中心的个数，通常可以采用 4096, 或者 16384
适用场景：候选向量集较少（如 50 万以内），且内存资源充足
是否支持 GPU：支持，GpuIndexFlat
是否需要训练：是，因为倒排索引需要训练k-means，因此需要先训练index，再add向量

1
2
3
4
5
6
7
8
9


dim, measure = 64, faiss.METRIC_L2 
# 代表k-means聚类中心为100
param = 'IVF100,Flat'                            
index = faiss.index_factory(dim, param, measure)
# 此时输出为False，因为倒排索引需要训练k-means，
print(index.is_trained)       
# 因此需要先训练index，再add向量
index.train(xb)                                  
index.add(xb)        

PQx ：乘积量化

向量维度切分
- 假设有一个高维向量 $V \in \mathbb{R}^D$，其中 $D$ 是向量维度。
- 将向量 $V$ 均匀切分为 $x$ 个子向量 $V_1, V_2, \dots, V_x$，每个子向量的维度为 $\frac{D}{x}$。
子空间量化
- 对每个子向量 $V_i$ 分别进行 k-means 聚类，生成每个子空间的量化码本（codebook）。
- 每个子空间的码本包含 $m$ 个聚类中心，称为 codewords。
- 每个子向量 $V_i$ 用其最近的 codeword 表示，得到一个索引 $q_i$，从而将原始向量 $V$ 压缩为 $x$ 个索引 $q_1, q_2, \dots, q_x$。
检索过程
- 查询向量切分：将查询向量 $Q$ 同样切分为 $x$ 个子向量 $Q_1, Q_2, \dots, Q_x$。
- 子向量检索：对于每个子向量 $Q_i$，计算它与对应子空间中所有 codewords 的距离，得到一个距离表。
- 结果聚合：对于候选向量库中的每个向量：
  - 根据其 PQ 编码的索引 $q_1, q_2, \dots, q_x$，从距离表中查找对应的子向量距离。
  - 将所有子向量的距离累加，得到查询向量与候选向量的近似距离。
- Top-K 选择：根据近似距离对所有候选向量进行排序，选出 Top-K 最接近的向量。

优点：速度很快，而且占用内存较小，召回率也相对较高（切4段）
缺点：召回率相较于暴力检索，下降较多
适用场景：内存及其稀缺，并且需要较快的检索速度，不那么在意召回率
是否支持GPU：
是否需要训练：是，因为倒排索引需要训练k-means，因此需要先训练index，再add向量

1
2
3
4
5
6
7
8


dim, measure = 64, faiss.METRIC_L2 
param =  'PQ16' 
index = faiss.index_factory(dim, param, measure)
# 此时输出为False，因为倒排索引需要训练k-means
print(index.is_trained)                          
# 因此需要先训练index，再add向量
index.train(xb)                                 
index.add(xb)  

IVFxPQy：倒排乘积量化

IVFxPQy 是一种高效的向量检索方法，结合了倒排索引（IVF）和乘积量化（PQ）的优点，通过分阶段缩小搜索范围和量化向量进一步降低计算和存储成本。以下是其实现原理和流程的详细说明：

构建倒排索引（IVF）

聚类过程：
- 使用 k-means 算法将所有候选向量划分为 $x$ 个聚类中心（cluster centers）。
- 每个聚类中心挂载一个倒排列表（inverted list），记录属于该聚类的所有非中心向量。
存储结构：
- 每个候选向量被分配到最近的聚类中心，并存储在对应的倒排列表中。
- 向量与聚类中心的距离信息也可以被存储，用于后续检索。

乘积量化（PQ）压缩向量

向量切分：
- 将每个向量的维度 $D$ 均匀切分为 $y$ 个子向量，每个子向量的维度为 $\frac{D}{y}$。
子空间量化：
- 对每个子向量进行 k-means 聚类，生成每段的量化码本（codebook）。
- 每个子向量用其最近的 codeword 表示，得到一个索引。
存储结构：
- 原始向量被压缩为 $y$ 个索引，而不是完整的 $D$ 维向量，显著节省存储空间。

检索流程

查询向量处理：
- 将查询向量 $Q$ 同样切分为 $y$ 个子向量 $Q_1, Q_2, \dots, Q_y$。
- 对每个子向量 $Q_i$，计算它与对应子空间中所有 codewords 的距离，生成一个距离表。
倒排索引检索：
- 使用 IVF 找到查询向量 $Q$ 最近的 $nprobe$ 个聚类中心（nprobe 是用户设定的参数）。
- 从这些聚类中心对应的倒排列表中获取候选向量。
近似距离计算：
- 对于每个候选向量：
  - 根据其 PQ 编码的索引 $q_1, q_2, \dots, q_y$，从距离表中查找对应的子向量距离。
  - 将所有子向量的距离累加，得到查询向量与候选向量的近似距离。
Top-K 选择：
- 根据近似距离对所有候选向量进行排序，选出 Top-K 最接近的向量。

优点

速度快：
- 通过 IVF 缩小搜索范围，仅检索最近的 $nprobe$ 个聚类中心下的向量，减少候选集数量。
- 通过 PQ 压缩向量，降低了距离计算复杂度。
内存占用小：
- PQ 将向量压缩为多个索引，显著节省存储空间。
召回率高：
- 结合 IVF 和 PQ，召回率接近暴力检索（Flat），同时显著提升检索速度。
灵活性：
- 可以根据需求调整 $x$（聚类中心数量）、$y$（切分段数）和 $nprobe$（检索的聚类中心数量），平衡性能和召回率。

参数说明

IVFx 中的 $x$：
- 表示 k-means 聚类中心的数量。
- $x$ 越大，每个聚类中心下挂载的向量数量越少，检索速度越快，但聚类精度可能下降。
PQy 中的 $y$：
- 表示将向量维度切分的段数。
- $y$ 越大，量化误差越小，召回率越高，但计算和存储成本也越高。
nprobe：
- 表示检索时搜索的聚类中心数量。
- 增大 nprobe 会提升召回率，但也会降低检索速度。

代码

1
2
3
4
5
6
7
8


dim, measure = 64, faiss.METRIC_L2  
param =  'IVF100,PQ16'
index = faiss.index_factory(dim, param, measure) 
# 此时输出为False，因为倒排索引需要训练k-means， 
print(index.is_trained)        
# 因此需要先训练index，再add向量 index.a
index.train(xb)                                  
index.add(xb)

LSH：局部敏感哈希

局部敏感哈希（LSH）是一种用于近似最近邻搜索（Approximate Nearest Neighbor, ANN）的哈希方法，其核心思想是利用哈希函数将高维空间中的相近向量映射到相同的哈希桶中，从而加速检索。以下是其原理、优缺点和适用场景的详细说明：

原理

哈希函数设计：
- LSH 的核心是设计一组哈希函数 $H$，使得在高维空间中距离较近的向量被映射到同一哈希桶的概率较高，而距离较远的向量被映射到同一哈希桶的概率较低。
分桶与碰撞：
- 对于每个向量 $V$，通过哈希函数 $H$ 计算其哈希值，并根据哈希值将其分配到对应的哈希桶中。
- 如果两个向量 $V_1$ 和 $V_2$ 的距离很近，则它们哈希值相同的概率（即哈希碰撞的概率）很高。
检索流程：
- 对于查询向量 $Q$：
  - 使用哈希函数 $H$ 计算其哈希值。
  - 查找哈希值对应的哈希桶，取出桶中的候选向量。
  - 对候选向量进行精确距离计算，选出 Top-K 最接近的向量。

优点

训练速度快：LSH 不需要复杂的模型训练，只需生成哈希函数，因此训练过程非常快。
支持分批导入：向量可以分批导入且无需重新训练，适合大规模数据集的动态更新。
内存占用小：只需存储哈希表和各向量的哈希值，内存占用较小。
检索速度快：通过哈希表快速定位候选向量，减少了实际距离计算的次数。

缺点

召回率低：LSH 是一种近似方法，召回率通常较低，尤其是当向量分布复杂或维度较高时。
参数敏感：哈希函数的数量和设计对召回率影响较大，需要反复调参。
哈希冲突问题：距离较远的向量也可能被映射到同一哈希桶中，导致候选集中包含无关向量。
时延不理想：在候选语料比较多的时候（百万级别），检索也不是特别快，大概是秒级别的。

适用情况

候选向量库非常大：LSH 适合处理大规模数据集，能够显著减少检索时间。
离线检索：LSH 的召回率较低，通常用于对召回率要求不高的离线检索场景。
内存资源稀缺：LSH 的内存占用较小，适合内存资源受限的场景。

代码

1
2
3
4
5
6


dim, measure = 64, faiss.METRIC_L2  
param =  'LSH'
index = faiss.index_factory(dim, param, measure) 
# 此时输出为True
print(index.is_trained)                          
index.add(xb)    

HNSW：分层的可导航小世界

Delaunay图

定义: Delaunay图（Delaunay三角剖分）是将平面上的一组点集进行三角剖分，确保所有三角形的最小角最大化。其核心性质是任何三角形的外接圆内不包含其他点。
构造方法: 常用的构造方法是Bowyer-Watson算法，通过逐步插入点并调整三角剖分，最终生成Delaunay图。
优点: 保证了点集间的连通性，任意两点之间存在通路。
缺点: 完整构造Delaunay图的复杂度较高，且在高维空间中效率较低，实际应用中难以直接使用。

NSW算法 (Navigable Small World)

背景: NSW算法是Delaunay图的近似优化，旨在降低构造复杂度并提高检索效率。
核心思想: 不像Delaunay图那样严格构造三角剖分，而是通过“高速公路”式的连接方式，使得检索时可以更快地接近目标点。
构造方法:
1. 从候选节点中随机选择一个节点。
2. 插入该节点并连接到其最近的若干个邻居节点。
特点: 检索速度快，但返回的结果是近似解，无法保证完全精确（groundtruth）。

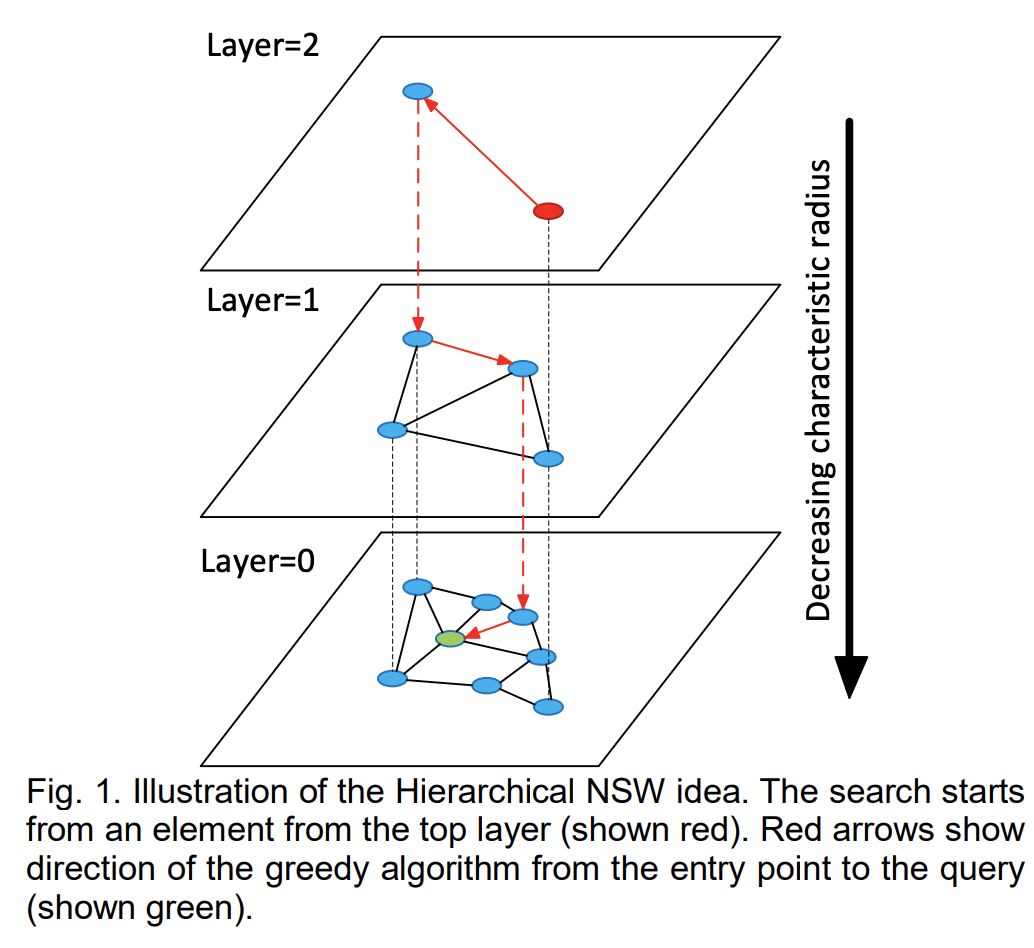
HNSW算法 (Hierarchical Navigable Small World)

背景: HNSW算法是对NSW算法的进一步优化，引入分层结构（类似跳表）以加速检索
核心思想:
- 构建多层图结构，每一层是前一层的一个子集，节点数量呈指数衰减
- 检索时从顶层开始，逐步向下层细化搜索，最终找到目标节点
构造方法:
1. 初始化:
  - 设定最大层数（maxLayer），并通过随机函数决定每个节点的层数
  - 节点层数服从指数衰减分布，高层的节点数量较少
2. 逐层插入节点:
  - 从最高层开始，逐层向下插入节点
  - 在每一层中，找到与新节点最接近的邻居，并建立连接（边）
  - 每层的邻居数量由参数M（最大邻居数）控制
3. 动态调整:
  - 如果某层的节点数超过一定阈值，则将该节点分配到下层
4. 重复上述过程，直到所有节点都被插入到图中
检索方法：HNSW的检索过程是一个自上而下的过程
1. 从顶层开始：- 在最高层（最稀疏的层）找到与查询点最接近的节点（起始点）。
2. 逐层向下搜索：在当前层中，找到与查询点最接近的若干个邻居节点。以下层的这些邻居节点为起点，继续搜索。
3. 底层精确搜索：在最底层（Layer 0）找到与查询点最接近的节点，作为最终结果。

优点

不需要训练：HNSW是一种基于图检索的算法，无需像机器学习模型那样进行训练，直接构建索引即可使用。
检索速度极快：在10亿级别的数据集上，HNSW能够在秒级返回检索结果，时间复杂度为O(log N)，甚至接近O(log log N)，几乎不受候选向量的量级影响。
召回率高：召回率接近Flat（暴力搜索），能达到97%以上，适合对精度要求较高的场景。
支持动态分批导入：支持分批导入数据，适合线上任务，能够实现毫秒级别的实时响应。
适应高维数据：在高维数据上表现优异，能够有效缓解“维度灾难”问题。

缺点

构建索引慢：构建索引的时间较长，尤其是在大规模数据集上，可能需要数小时甚至更长时间。
占用内存大：HNSW的内存占用较高，其索引大小通常大于原始向量占用的内存，是Faiss中内存占用最大的算法之一。
不支持指定数据ID：添加数据时无法指定数据ID，限制了某些特定场景的使用。
不支持删除数据：不支持从索引中删除数据，如果需要删除数据，必须重新构建索引。
不支持GPU加速：HNSW的实现主要依赖CPU，目前不支持GPU加速，因此在处理超大规模数据时可能受限于硬件性能。

HNSW参数：`x`（`M`）的作用

在HNSW算法中，x（通常用参数M表示）是一个关键参数，用于控制图构建时每个节点最多连接的邻居节点数量。这个参数直接影响图的结构、检索精度以及构建和检索的效率。以下是M的详细解析:

`M`的含义

M：构建图时每个节点最多连接的邻居节点数量。
取值范围：通常为4到64之间的整数。
默认值：不同实现中默认值可能不同，例如在Faiss中，M的默认值为16。

`M`的影响

对图结构的影响:
- M越大，每个节点的连接数越多，图的密度越高，节点之间的连通性越好。
- M越小，图的密度越低，节点之间的连通性越差。
对构建时间的影响:
- M越大，构建图时需要计算的邻居连接越多，构建时间越长。
- M越小，构建时间越短。
对检索精度的影响:
- M越大，图的连通性越好，检索时可以找到更精确的最近邻点，召回率越高。
- M越小，图的连通性越差，检索精度可能降低。
对检索速度的影响:
- M越大，检索时需要遍历的邻居节点越多，检索速度可能变慢。
- M越小，检索时需要遍历的邻居节点越少，检索速度可能加快。

适用情况

不在乎内存：如果系统内存资源充裕，能够承受较大的内存开销，HNSW是一个很好的选择。
有充裕的时间构建索引：如果对索引构建时间没有严格要求，且更注重检索速度和召回率，HNSW非常适合。
高精度检索需求：适用于对检索精度要求较高（召回率接近暴力搜索）的场景，如推荐系统、图像检索等。
实时检索任务：支持分批导入和实时检索，适合需要毫秒级响应的线上任务。

代码

1
2
3
4
5
6


dim, measure = 64, faiss.METRIC_L2   
param =  'HNSW64' 
index = faiss.index_factory(dim, param, measure)  
# 此时输出为True 
print(index.is_trained)                          
index.add(xb)

Faiss 参数总结

dim（向量维数）

param（索引参数）

measure（度量方法）

索引构建与检索的常见流程

Flat ：暴力检索

IVFx Flat ：倒排暴力检索

PQx ：乘积量化

IVFxPQy：倒排乘积量化

构建倒排索引（IVF）

乘积量化（PQ）压缩向量

检索流程

优点

参数说明

代码

LSH：局部敏感哈希

原理

优点

缺点

适用情况

代码

HNSW：分层的可导航小世界

Delaunay图

NSW算法 (Navigable Small World)

HNSW算法 (Hierarchical Navigable Small World)

优点

缺点

HNSW参数：x（M）的作用

M的含义

M的影响

适用情况

代码

`dim`（向量维数）

`param`（索引参数）

`measure`（度量方法）

HNSW参数：`x`（`M`）的作用

`M`的含义

`M`的影响